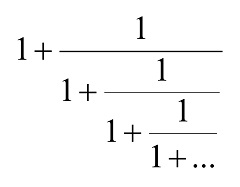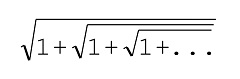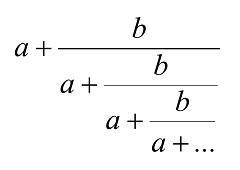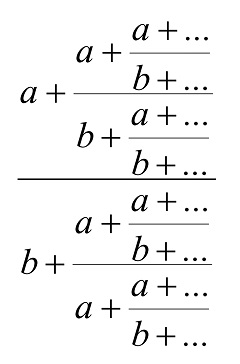EXPRESIONES FRACTALES

“Los fractales son el medio más simple de crear complejidad” (Jorge Wagensberg)

“La geometría de la naturaleza tiene una cara fractal” (Mandelbrot)

“La fractalidad prioritariamente coloniza. Es una manera de llenar el espacio, es una manera de crecer” (Jorge Wagensberg)

---

Definición

Un fractal es un gráfico recursivo en el que un mismo patrón, que es el propio gráfico completo, se repite en los diferentes niveles. Análogamente, una expresión fractal es un tipo de expresión recursiva multinivel en la que en uno o varios puntos de cada nivel se hace referencia a la expresión original, de tal manera que el mismo patrón (la expresión completa) se repite en esos puntos. Estos puntos se denominan “autorreferencias”. Las expresiones fractales se llaman también “expresiones autorreferenciadas”.

Una expresión fractal puede tener una o varias autorreferencias y un número finito o infinito de niveles. Veamos algunos ejemplos.


Expresiones aritméticas fractales

1. La proporción aúrea (1.618…) equivale al valor de la expresión fractal de una autorreferencia de infinitos niveles
   
   
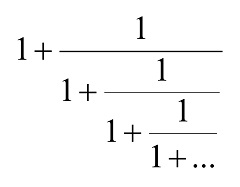
   Esta expresión es un ejemplo de lo que en matemática se denomina fracción continua, y puede expresarse de forma recursiva así:
   
   
   (Φ =: (1 + 1.÷Φ))
   
   
2. Otra forma equivalente de expresar la proporción aúrea es mediante la expresión fractal (también de una autorreferencia y de infinitos niveles)
   
   
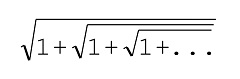
   y puede expresarse de forma recursiva así:
   
   (Φ =: (1.+Φ)v2) // (xvy es y√x)
   
   
3. La raíz cuadrada de 2 (r) se puede expresar de forma recursiva:
   
   ( r =: (1 + 1.÷(1+r)) )
   
   
4. (x =: a + b÷x)
   
   Esta es una expresión aritmética con una autorreferencia y de infinitos niveles. Representa a la fracción continua
   
   
   
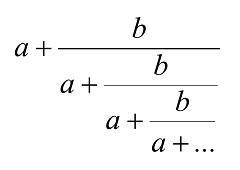
5. (x =: (a+x)÷(b+x))
   
   Esta es una expresión aritmética con dos autorreferencias y de infinitos niveles. Su expansión produciría una fracción continua de la forma
   
   
   
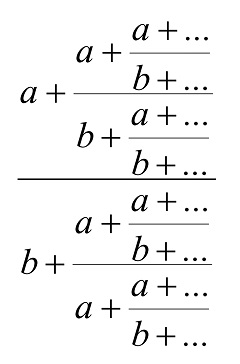
6. (s = “Esta sentencia tiene cinco palabras”)
   
   ( s =: (s# = 5) ), que representa a la expresión fractal
   
   (((s# = 5)# = 5)# = 5)#...

Secuencias fractales

1. (x =: axbx)
   
   Este ejemplo contiene dos autorreferencias. Los diferentes niveles son los siguientes:
   
   (axbx)
a(axbx)b(axbx)
a(a(axbx)b(axbx))b(a(axbx)b(axbx))
   ...
   
   
2. (x =: (a x b)) // rep. (a (a (a ... b) b) b)))
   
   
3. (x =: (a b x)) // rep. (a b (a b (a b (...))))
   
   
4. (x =: (a x↓ b)) // rep. (a a a ... b b b)
   
   
5. (x =: (a b x↓)) // rep. (a b a b a b ...)

Conjuntos fractales

1. ⟨( c =: {a c b} )⟩ // rep. {a {a {a ...} b} b} b}}
   
   
2. (x =: {x}) // x rep. ...{{{}}}...
   
   
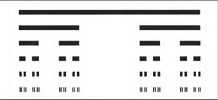
3. Conjunto de Cantor (o polvo de Cantor)
   
   

   Polvo de Cantor

   
   ⟨( cantor(r1_r2) =: ( cantor(r1_(r1 + (r2−r1)¸3) cantor(r2−(r2−r1)¸3)_r2) ) )⟩
   
   (r1_r2 es un rango continuo que representa a los números reales entre r1 y r2.)

Especificación general de expresiones fractales finitas

Los ejemplos anteriores corresponden a expresiones fractales de infinitos niveles y en donde cada autorreferencia es la misma expresión original. Pero podemos especificar de forma general expresiones fractales de un número determinado de niveles.

Si llamamos:

• p al patron de la expresión fractal (expresión inicial).
• v a la subexpresión de p a expandir (normalmente es una variable dentro del patrón).
• n al número de niveles.

tenemos la siguiente expresión general de una expresión fractal de una variable:

⟨( fractal(p v n) = (p ← n=1 →' (p = p/(v=p) fractal(p v n−1) )⟩

Ejemplo: Proporción áurea expresada como fracción continua.

fractal((1 + 1.÷Φ) Φ 1) // ev. (1 + 1.÷Φ)
fractal((1 + 1.÷Φ) Φ 2) // ev. (1 + 1÷(1 + 1.÷Φ))
fractal((1 + 1.÷Φ) Φ 3) // ev. (1 + 1÷(1 + 1÷(1 + 1.÷Φ)))
...